كيفية حساب قانون محيط المثلث بدقة

يُعد علم الهندسة من أهم فروع الرياضيات التي تساعدنا على فهم الأشكال والمسافات من حولنا، ومن بين أبرز مفاهيمه قانون محيط المثلث. هذا القانون يتيح لنا حساب مجموع أطوال أضلاع أي مثلث بسهولة، مما يجعله أساسياً في العديد من التطبيقات اليومية والهندسية. سواء في تصميم المباني أو حل المسائل الرياضية، فإن فهم قانون محيط المثلث يعزز القدرة على التحليل والدقة، ويعتبر من المهارات الضرورية للطلاب في مختلف المراحل التعليمية.

ما هو قانون محيط المثلث؟

عند دراسة الأشكال الهندسية. يعد المثلث من أكثر الأشكال شيوعًا في مختلف فروع الرياضيات والهندسة. ومن المهم التفرقة بين المفاهيم الأساسية المتعلقة به. مثل المحيط والمساحة. وبالانتقال إلى مفهوم قانون محيط المثلث. فهو ببساطة يعتمد على جمع أطوال أضلاع المثلث الثلاثة. أي: المحيط = الضلع الأول + الضلع الثاني + الضلع الثالث. يستخدم هذا القانون في حساب المسافة الخارجية حول المثلث. وهو ضروري في العديد من التطبيقات العملية.

من جهة أخرى. فإن مساحة المثلث تحسب بطريقة مختلفة تمامًا. حيث يتم استخدام القاعدة والارتفاع في القانون الأساسي. أو يمكن استخدام صيغة هيرون في بعض الحالات. ومن هنا نلاحظ أهمية فهم الفرق بين المحيط والمساحة لتطبيق كل منهما بشكل صحيح في المواقف المختلفة.

تعرف ايضًا على: شرح مفصل عن ما هو الوسط الحسابي

كيف أجد المحيط المثلث؟

إذا كنتِ تتساءلين كيف أجد محيط المثلث؟ فالإجابة تعتمد أولًا على نوع المثلث وأطوال أضلاعه. بشكل عام. يتم حساب المحيط بجمع أطوال الأضلاع الثلاثة. وهي طريقة بسيطة لكنها تتطلب معرفة دقيقة بقياسات الأضلاع.

ولفهم الطريقة بشكل أوضح. دعينا ننتقل إلى مثال عملي على محيط المثلث القائم. هذا النوع من المثلثات يحتوي على زاوية قائمة (90 درجة). ويمكن استخدام نظرية فيثاغورس لمعرفة الضلع الثالث إذا كان غير معروف. ثم جمع الأضلاع الثلاثة للحصول على المحيط.

باختصار. فإن قانون محيط المثلث يظل ثابتًا لكل الأنواع. وهو: المحيط = مجموع أطوال الأضلاع. لكن طريقة تطبيقه قد تختلف تبعًا لنوع المثلث والمعطيات المتوفرة.

تعرف ايضًا على: خطوات تطبيق قانون الجذب في الحياة العملية

ما هي مساحة المثلث ومحيطه؟

عند الحديث عن محيط المثلث ومساحته. من المهم أولًا أن نميز بين المفهومين. فالمحيط يشير إلى الطول الكلي لجميع أضلاع المثلث. بينما المساحة تمثل مقدار السطح الذي يغطيه الشكل داخل حدوده.

ولحساب المساحة. توجد أكثر من طريقة. لكن الطريقة الأكثر شيوعًا هي استخدام القاعدة × الارتفاع ÷ 2. وتناسب هذه الطريقة المثلثات التي نعرف فيها طول القاعدة والارتفاع العمودي عليها. أما إذا كانت أطوال الأضلاع الثلاثة معروفة. يمكننا استخدام صيغة “هيرون”.

أما عن قانون محيط المثلث. فهو ببساطة: مجموع أطوال الأضلاع الثلاثة. على سبيل المثال. إذا كان لدينا مثلث أطوال أضلاعه 5. 6. و7 سم. فإن محيطه يساوي 5 + 6 + 7 = 18 سم.

وهكذا. باستخدام هذه القوانين البسيطة. يمكنكِ بسهولة حساب كل من المحيط والمساحة لأي مثلث. بشرط توفر المعطيات الأساسية.

تعرف ايضًا على: شرح قانون نيوتن الثاني للحركة

كيف أحسب محيط مثلث متساوي الأضلاع؟

لحساب محيط مثلث متساوي الأضلاع. يجب أولًا معرفة خاصية أساسية فيه. وهي أن جميع أضلاعه متساوية في الطول. وبالتالي. تكون الطريقة بسيطة للغاية؛ إذ يكفي أن نضرب طول أحد الأضلاع في 3. على سبيل المثال. إذا كان طول أحد الأضلاع 6 سم. فإن المحيط = 6 × 3 = 18 سم.

ومن ناحية أخرى. تختلف طريقة الحساب عندما يكون المثلث غير منتظم. أي أن أطوال أضلاعه غير متساوية. وهنا يأتي دور قانون محيط المثلث الذي يعتمد على جمع أطوال الأضلاع الثلاثة دون الحاجة لأي شروط إضافية.

وفي سياق المقارنة. إذا أردت حساب محيط المثلث مختلف الأضلاع. فما عليك سوى معرفة أطوال الأضلاع الثلاثة وجمعها معًا. مما يجعل الأمر سهلًا لكنه يتطلب دقة في تحديد الأطوال. باختصار. نوع المثلث يحدد طريقة الحساب. لكن الفهم الأساسي للقانون يسهّل التعامل مع جميع الأشكال.

تعرف ايضًا على: القوانين الأساسية لنيوتن في الحركة

ما هو قانون محيط المثلث متساوي الساقين؟

عند الحديث عن قانون محيط المثلث متساوي الساقين. لا بد أولًا من فهم خصائص هذا النوع من المثلثات. يتميز المثلث متساوي الساقين بأن له ضلعين متساويين في الطول. وقاعدة تختلف عنهما. وبناءً على ذلك. فإن المحيط يُحسب من خلال جمع طولي الساقين مع طول القاعدة.

ولتوضيح الأمر بشكل أكبر. لنفترض أن طول كل ساق 5 سم. والقاعدة 4 سم. فإن المحيط سيكون: 5 + 5 + 4 = 14 سم.

ومن ناحية أخرى. يمكنك استخدام قانون محيط المثلث بشكل عام مع هذا النوع أيضًا. لأنه ببساطة يعتمد على جمع أطوال الأضلاع الثلاثة. سواء كانت متساوية أم لا. وهكذا. نجد أن معرفة خصائص المثلث أولًا. ثم تطبيق القانون المناسب ثانيًا. يسهّل علينا حساب المحيط بدقة وسرعة.

تعرف ايضًا على: أسباب ونتائج الإحتباس الحراري

قانون مساحة المثلث القائم

عند الحديث عن مساحة المثلث القائم. فإننا نعتمد على قاعدة رياضية بسيطة ومباشرة. وهي أن المساحة تحسب بضرب القاعدة في الارتفاع ثم قسمة الناتج على 2. وفي حالة المثلث القائم. تمثل الضلعين اللذين يشكلان الزاوية القائمة (القاعدة والارتفاع) القيم المطلوبة للحساب. على سبيل المثال. إذا كانت القاعدة 6 سم والارتفاع 4 سم. فإن المساحة = (6 × 4) ÷ 2 = 12 سم².

لكن من المهم أيضًا ألا نغفل عن قانون محيط المثلث. حتى وإن كان التركيز هنا على المساحة. لأن معرفة المحيط قد تكون مفيدة في مسائل أكثر تعقيدًا تتعلق بحساب المسافة حول الشكل.

وباختصار. يعتبر فهم خصائص المثلث القائم وتطبيق القوانين الرياضية المرتبطة به أمرًا أساسيًا لكل من يرغب في إتقان أساسيات الهندسة.[1]

تعرف ايضًا على: لاوحدة قياس الكثافة في الفيزياء

قوانين محيط المثلث القائم ومساحته

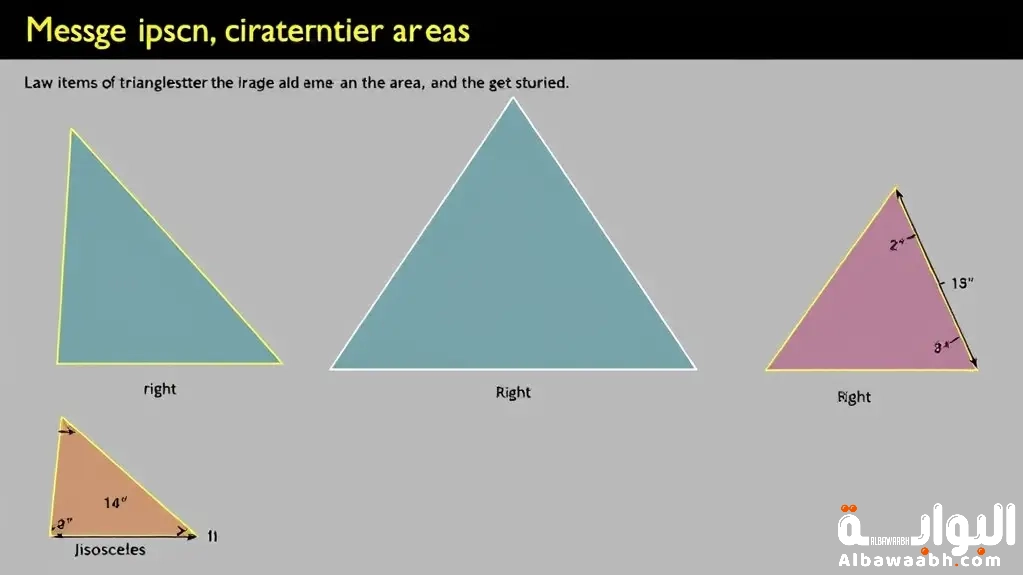
لفهم محيط المثلث القائم ومساحته. علينا أولًا التعرف على خصائص هذا النوع من المثلثات. المثلث القائم يحتوي على زاوية قائمة (90 درجة). مما يجعل من السهل تطبيق القوانين الهندسية عليه. بالنسبة للمساحة. فإنها تُحسب من خلال ضرب طول القاعدة في الارتفاع ثم قسمة الناتج على 2. وهي قاعدة أساسية تنطبق على جميع المثلثات. وبشكل خاص على القائم لأنه يسهل تحديد أبعاده.

أما قانون محيط المثلث القائم. فيعتمد على جمع أطوال الأضلاع الثلاثة. بما في ذلك الوتر. وهو الضلع المقابل للزاوية القائمة. على سبيل المثال. إذا كانت أطوال الضلعين القائمين 3 و4. فإن الوتر (حسب فيثاغورس) يكون 5. فيصبح المحيط 3 + 4 + 5 = 12 وحدة. ومن خلال هذه القوانين البسيطة. يمكن لأي طالب أو مهتم بالرياضيات أن يفهم ويحسب بسهولة محيط ومساحة أي مثلث قائم. مما يعزز فهمه للموضوع بطريقة واضحة ومنظمة.[2]

في الختام، يعتبر قانون محيط المثلث من القوانين البسيطة في صيغته، لكنه بالغ الأهمية في الاستخدام العملي والنظري. فبمجرد جمع أطوال الأضلاع الثلاثة نحصل على المحيط، وهي خطوة أساسية لفهم أعمق للخصائص الهندسية للأشكال. إن إتقان قانون محيط المثلث لا يساعد فقط في حل المسائل المدرسية، بل يُشكل أيضاً مدخلاً لتطبيقات واسعة في مجالات التصميم، والعمارة، والهندسة، مما يبرز قيمته في الحياة العلمية والعملية.

• byjusLaw of area of a right triangle _بتصرف
• tutoraxLaws of the perimeter and area of a right triangle _بتصرف

مشاركة المقال

وسوم