كيفية حساب محيط المثلث

الكاتب : حبيبة دراز

التعليم

20 يناير 2026

عدد المشاهدات : 1509

منذ أسبوعين

أنواع المثلثات

أنواع المثلثات بالنسبة للزوايا:

أنواع المثلثات بالنسبة للأضلاع:

المثلث متساوي الأضلع:

المثلث متساوي الضلعين:

المثلث غير متساوي الأضلع:

أنواع المثلثات بالنسبة للأضلع والزوايا:

ما المقصود بمحيط المثلث؟

كيفية حساب محيط المثلث

حساب محيط المثلث قائم الزاوية ومتساوي الضلعين

الأسئلة الشائعة

ما هو محيط المثلث؟

هل تختلف طريقة حساب محيط المثلث حسب نوعه؟

ما وحدة قياس محيط المثلث؟

هل يمكن حساب محيط المثلث إذا كان أحد الأضلاع مجهولًا؟

كيفية حساب محيط المثلث من أساسيات علم الرياضيات التي يحتاجها الطلاب في مختلف المراحل الدراسية. يساعد فهم طريقة حساب محيط المثلث على حل العديد من المسائل الهندسية والتطبيقات العملية بسهولة ودقة.

أنواع المثلثات

يوجد مثلثات كثيرة مختلفة الأشكال والأطوال.علاوة على ذلك تم تقسيم هذه المثلثات لعدة أنواع على طبقا لمعيارين، وهما:

أنواع المثلثات بالنسبة للزوايا:

المثلث الحاد :

وهو المثلث الذي يكون قياس زواياه أقل من تسعون درجة. كالمثلث ( أ ب ج )، ذو الزوايا 60 درجة، 50 درجة، 40 درجة.

تعرف أيضًا على: دراسة ما هي طاقة الرياح وكيفية استخدامها

المثلث منفرج الزاوية:

المثلثات منفرجات الزاوية هي المثلثات التي تحتوي على زاوية واحدة قياسها أكبر من تسعون درجة. كالمثلث ( أ ب ج )، والذي قياس زواياه هي 50 درجة، 20 درجة. بالإضافة الى ذلك الزاوية المنفرجة ذات المئة درجة.

المثلث قائم الزاوية:

وهذه المثلثات تحتوي على زاوية قائمة. بالإضافة الى ذلك الزاوية القائمة هي الزاوية التي يكون قياسها تسعون درجة تماما.

أنواع المثلثات بالنسبة للأضلاع:

المثلث متساوي الأضلع:

المثلثات متساوية الأضلع الثلاثة هي المثلثات التي يكون كل أطوال أضلاعها الثلاثة متساوية ومتطابقة، كالمثلث طول ضلعه الأول هو خمسون سنتي مترا، وطول ضلعه الثاني خمسون سنتي مترا، وطول ضلعه الثالث والأخير هو خمسون سنتي مترا أيضا.

المثلث متساوي الضلعين:

وهو المثلث الذي يكون قياس طول ضلعين من أضلاعه الثلاثة متساوي. علاوة على ذلك كأن يكون طول ضلعه الأول عشرون سنتي مترا. بالإضافة الى ذلك الثاني عشرون سنتي مترا.بالإضافة الى ذلك الثالث مختلف فيكون قياس طوله يساوي ثلاثون سنتي مترا.

تعرف أيضًا على: كيفية حساب قانون محيط المثلث بدقة

المثلث غير متساوي الأضلع:

وهو المثلث الذي يكون أطوال أضلاعه الثلاثة مختلفين غير متساوين في أطوالهم. بالإضافة الى ذلك يكون قياس طول الضلع الأول هو خمسة وعشرون سنتي مترا. طول الضلع الثاني هو خمسون سنتي مترا. بالإضافة الى ذلك طول الضلع الثالث والأخير هو عشرون سنتي مترا.

أنواع المثلثات بالنسبة للأضلع والزوايا:

أولا المثلث متساوي الأضلع أو متساوي الزوايا:

هو الذي تكون أطوال أضلعه متساوية. بالإضافة الى ذلك قياس زواياه متساوية أيضا.

ثانيًا المثلث قائم الزاوية ومتساوي الضلعين:

وهو المثلث الذي يكون طول ضلعين من أطلاعه متساوية.بالإضافة الى ذلك يكون ذو زاوية قائمة. علاوة على ذلك أي زاوية تكون قياسها يساوي التسعون درجة.

ثالثًا المثلث متساوي الضلعين ومنفرج الزاوية:

هو المثلث الذي يكون لدية ضلعين من أضلاعه متساويين، وذو زاوية منفرجة. علاوة على ذلك أي زاوية يكون قياسها أكبر من تسعون درجة.

تعرف أيضًا على: شرح مفصل عن ما هو الوسط الحسابي

رابعا المثلث متساوي الضلعين الحاد:

وهو المثلث الذي يكون جميع زواياه حادة. أي قياسها أقل من تسعون درجة، ويكون له ضلعين متساويين في الطول.

خامسًا المثلث مختلف الأضلع قائم الزاوية:

هو المثلث الذي يمتلك زاوية واحدة قائمة. بالإضافة الى ذلك وتكون أطوال أضلاعه الثلاثة مختلفة.

سادسًا المثلث مختلف الأضلع منفرج الزاوية:

وهو المثلث الذي يحتوي على زاوية واحدة منفرجة؛ أي أكبر من تسعون درجة. بالإضافة الى ذلك تكون قياس أطوال جميع أضلعه مختلفة.

سابعا المثلث مختلف الأضلع حاد الزوايا:

وهو المثلث الذي تكون جميع زواياه حادة؛ أي أن يكون قياسها أقل من تسعون درجة، ويكون جميع أطوال أضلاعه الثلاثة مختلفة وغير متساوية. [1]

ما المقصود بمحيط المثلث؟

المحيط للأشكال ثنائية الأبعاد هو المسافة حلول هذا الشكل، ويمككنا حساب محيط أي شكل بحساب أطوال أضلاعه، وفي حالة المثلث باختلاف أنواعه فهو طول المسافة حول المثلث؛ أي أطوال أطلاع المثلث الثلاثة مجموعة مع بعضهم البعض، بإيجاز

تعرف أيضًا على: خطوات تطبيق قانون الجذب في الحياة العملية

المحيط = مجموع أطوال المثلث الثلاثة،أو يمكننا كتابتها بهذا الشكل:

P = a+b+c ، فتكون P رمز للمحيط (Perimeter) و a تمثل طول الضلع الأول، و b تمثل طول الضلع الثاني، و c تمثل طول الضلع الثالث، ومن المهم ألا تنسى كتابة وحدة القياس وإضافتها لإجابتك في النهاية. [2]

كيفية حساب محيط المثلث

يختلف حساب محيط كل مثلث عن الأخر، تبعا لنوع المثلث، فلكل نوع كيفية مختلفة، ونوضح هذه الكيفيات المختلفة، وهي:

أ. أولا حساب محيط المثلث غير متساوي الأضلاع:

يتم حساب محيط المثلث غير متساوي الأضلاع عن طريق جمع أطوال أضلاعه الثلاثة غير المتساوية.

باستخدام الصيغة: المحيط (P) = أ + ب + ج ، حيث (أ) و(ب) و(ج) هي أطوال أضلع المثلث الثلاثة.

ب. ثانيًا حساب محيط المثلث متساوي الضلعين:

تعرف أيضًا على: ماذا يعني ما هو قانون نيوتن الثاني

يتم حساب محيط المثلث متساوي الضلعين بواسطة إيجاد مجموع طول الضلعين المتساويين والضلع الثالث المختلف.

باستخدام الصيغة: المحيط (P) = 2أ + ب ، حيث (أ) ضلعان لهما نفس الطول، و(ب) الضلع الثالث المختلف طوله.

ج. ثالثًا حساب محيط المثلث متساوي الأضلع:

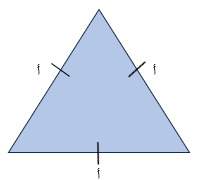
يتم حساب محيط المثلث الذي جميع أطوال أضلاعه متساوية بواسطة ضرب طول الضلع في ثلاثة.علاوة على ذلك وتكون صيغتها: المحيط = 3 x أ

د. رابعا حساب محيط المثلث قائم الزاوية:

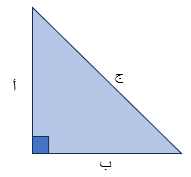
يتم حساب محيط المثلث قائم الزاوية بواسطة التعويض بالأضلع المعطاة، باستخدام الصيغة:

المحيط (P) = أ + ب + ج .

يمكن استخدام نظرية فيثاغورس في هذه الحالة. لآنه مثلث قائم الزاوية، باعتبار أن أحد أطوال هذا المثلث مجهولة.علاوة على ذلك ينص قانون فيثاغورس على أن مربع الوتر يساوي مجموع مربعي الضلعين الأخرين، حيث أن: (أ) ضلع عمودي على، و(ب) ضلع القاعدة.

تعرف أيضًا على: أهمية قانون حمورابي

و(ج) هو وتر المثلث قائم الزاوية، إذا فإن (2أ) = (2ب) + (2ج). وبالتالي يمكن كتابة محيط المثلث قائم الزاوية كالآتي: المحيط (P) = (أ) + (ب) + √(2أ + 2ب)، وذلك لأن 2ج= 2أ +2ب، وبالتالي ج= √(2أ + 2ب).

ه. حساب محيط مثلث قائم الزاوية ومتساوي الضلعين:

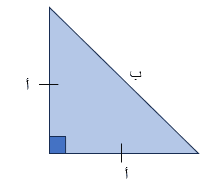
حساب محيط المثلث قائم الزاوية ومتساوي الضلعين

يتم حساب محيط المثلث قائم الزاوية ومتساوي الضلعين بواسطة جمع أطوال أضلاعه المعطاة. بالإضافة الى ذلك استخدام الصيغة: المحيط (P) = 2أ + ب، حيث (أ) هو طول الضلعين المتساويين في المثلث، و(ب) هو الوتر. علاوة على ذلك في حال كان أحدهما فقط هو المعطى يتم حلها باستخدام نظرية فيثاغورس. بالتالي فسبق وعلمنا أن (ب) = √(2أ + 2أ)، وبعد تبسيطها تصبح:

(ب) = √2 x أ ، أو (أ) = ب/ √2 .

وبعد الاستنتاجات السابقة يمكن حساب محيط المثلث قائم الزاوية ومتساوي الضلعين إذا كانت (أ) فقط هو المعلوم بواسطة الصيغة: المحيط (P) = 2أ + √2أ ، فاستبدلنا (ب) ب (√2أ). وكذلك يمكن حساب محيط المثلث قائم الزاوية ومتساوي الضلعين إذا كانت (ب) فقط هي المعلومة. علاوة على ذلك فتأتي ب(أ) بواسطة (أ) = ب/ √2 ، وتكون صيغة حساب المحيط: (P) = 2 (ب/ √2) + ب = (√2 x ب) + ب. [3]

في الختام، فإن كيفية حساب محيط المثلث تعد مهارة رياضية أساسية تسهّل فهم الهندسة وحل المسائل المختلفة. إتقان كيفية حساب محيط المثلث يساعد الطلاب على بناء أساس قوي في الرياضيات.